Model and Likelihood

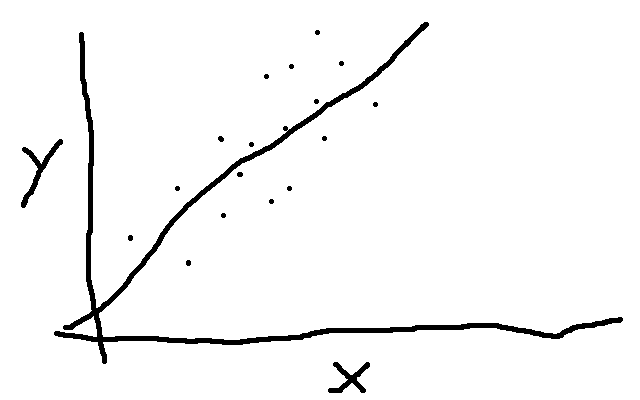
\[y = m * x + b\]

\[\mu = m * x + b\]

Likelihood

\[y = \mu + \epsilon\]

\[\epsilon \sim N(0, \sigma)\]

Parameters

• The slope, \(m\)

• The intercept, \(b\)

• The variability, \(\sigma\)

• Collectively, \(\theta\)

Likelihood

\[P(Y | \theta)\]

\[P(Y | \theta, X)\]

Prior

\[P(\theta)\]

Bayes Rule

\[P(\theta | Y) = \frac{P(Y|\theta)P(\theta)}{P(Y)}\]

Prior -> Posterior

\[P(\theta | Y)\]

Prior -> Posterior

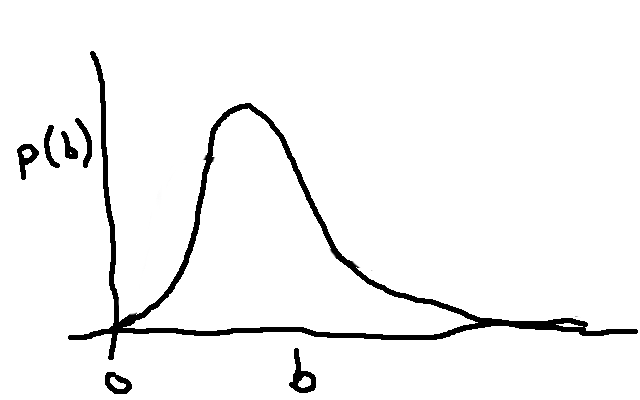
\[P(\theta | Y)\]

Using the posterior

The Denominator

\[P(\theta | Y) = \frac{P(Y|\theta)P(\theta)}{P(Y)}\]

Algorithms you may have heard of

• Metropolis-Hastings

• Gibbs

curve(dnorm(x), xlim = c(-3, 3)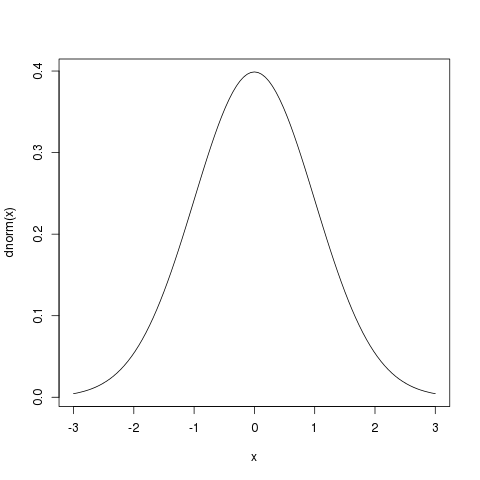

plot(density(rnorm(1000)), xlim = c(-3, 3))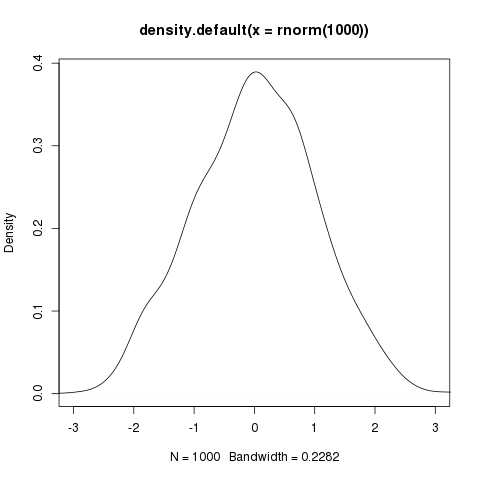

“Rejection sampling”

Sample from the joint distribution, \(P(\theta, Y) = P(\theta)P(Y|\theta)\)

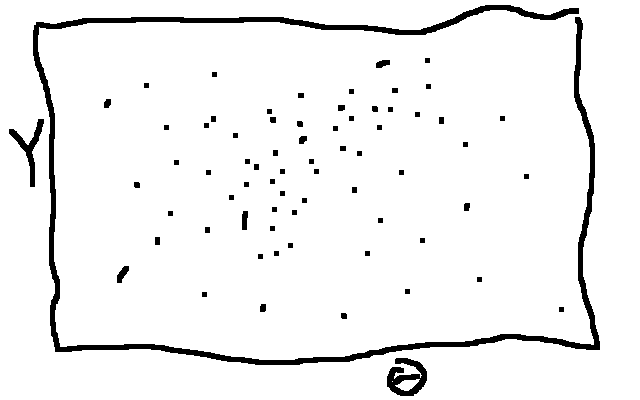
“Rejection sampling”

Reject when the sampled \(Y\) does not equal the observed

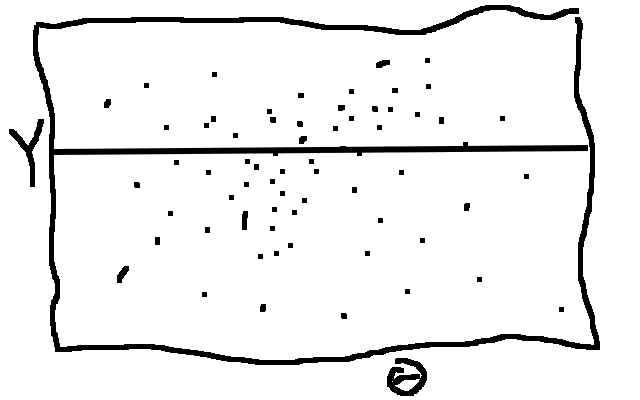
Algorithm

1. Sample \(\theta^*\) from the prior: \(P(\theta)\)
2. Sample \(Y^*\) from the likelihood: \(P(Y|\theta^*)\)
3. If \(Y^*\) is equal to the observed data, keep \(\theta^*\), if not reject.

Speeding it up

1. Summary statistics (perhaps sufficient)
2. Add some wiggle room

Why use ABC?

Cases where we can simulate data, we know the data generating process, but might have difficulty writing down a likelihood.

Basic idea

Write code in C++, call from R

Because C++ is faster than R

Not a new concept but Rcpp makes this much easier

How scared should I be of C++?

• Equal signs, not assignment arrows
• Semi-colons at the end of lines
• Indexing starts at 0
• For loops have a different structure
• Type definitions

Examples

• Addition
• Fibonacci sequence
• Multiple functions

uspop data in R

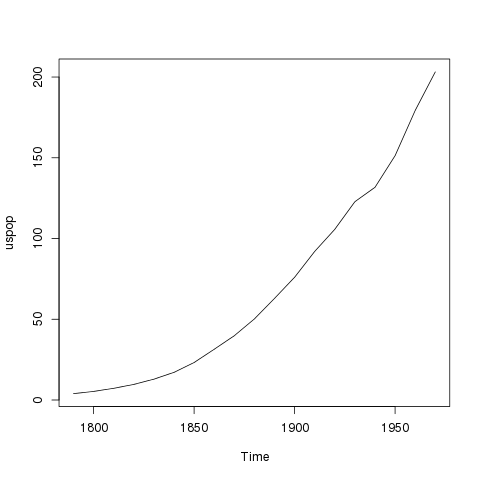
Proportional Growth

\[\frac{dp}{dt} = rp\]

\[p = p_0 e ^ {rt}\]

Logistic growth function

\[\frac{dp}{dt} = \frac{rp(K - p)}{K}\]

\[p = \frac{K}{1 + (K / p_0 - 1) e^ {- r t}}\]